Творчество - занятие нескучное, и более того, творить можно с юмором. Возможно,
эта задачка вам знакома. Возможно, вы, как и многие другие, думаете,
что есть только одно решение. Так забудьте его, и найдите новое.
Вот они – 9 магических точек:

Задача: не отрывая карандаша от бумаги, провести 4 пересекающиеся прямые линии, которые коснутся всех девяти точек только 1 раз.
Потратьте на поиск решения не менее 5 минут, прежде, чем читать дальше.
Если у вас ничего не вышло, подумайте о том, что вы видите, глядя на эти 9 точек? Если вы представляете себе квадрат, треугольники или другие геометрические фигуры, то вы блокируете свое мышление, рисуя границы, которых нет. Вы удерживаете себя внутри линий, которых не существует.
Привычка, сводящая креативность к нулю: мы слишком часто возводим границы, которых на самом деле нет. И мы остаемся в них. Мы играем по этим правилам. Мы пользуемся фантомными критериями. Мы прогнозируем развитие проекта, основываясь на тенденциях и возможностях, имевших место в прошлом, без поиска и сопоставления новых. Мы не отбрасываем сложившуюся парадигму без разрешения.
Вы могли бы соединить точки четырьмя линиями, выйдя за рамки квадрата. Вот так:
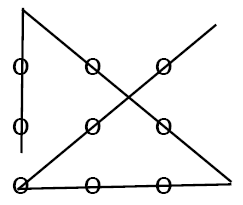
Как вам решение? Нравится? Не кажется ли оно вам элегантным и единственно возможным? На самом деле, самым серьезным ограничением в решении этой задачи является как раз вывод, что существует только ОДИН ответ. В действительности же вы можете отыскать несколько абсолютно разных решений этой проблемы.
Но как сломать парадигму и найти другие результаты?
Есть техника, которая называется «вынужденный уход». Нужно забыть о постановке проблемы и работать над решением ее дистанцированной версии. Это путь к новым парадигмам, перспективам и результатам.
И первой модифицированной задачей будет… те же 9 точек

Задача: на этот раз проведите 3 пересекающиеся прямые линии, которые должны коснуться каждой точки только 1 раз. Если не удается найти решение, постарайтесь определить, какие рамки, выводы и критерии вам мешают и останавливают поиск.
Давайте посмотрим вместе.
Во-первых, скажите, что вы видите, глядя на область точек? Надеюсь, вы уже отказались от привычки рисовать квадрат и другие фигуры. Теперь вас, возможно, блокирует то, что вы видите эти точки на листе бумаги. Для того, чтобы найти несколько способов решения проблемы «3 линий», вам нужно представить эти точек в пространстве. Только так 3 прямые смогут покинуть кусок бумаги.
Во, вторых, не кажется ли вам, что эти линии должны проходить через центр каждой из 9 точек? Это несуществующее условие мешает вам думать.
В-третьих, как вы определяете саму точку? В школе нас учили, что точка – это элемент геометрического пространства, характеризуется только положением, принадлежностью, а не размером или формой. А вот эти кружочки, которые в нашей задаче называются точками, как раз имеют и форму, и размер. Не совсем честно с нашей стороны, да? Ну что ж, такова жизнь. А в реальной жизни точки очень разнятся по величине и форме. На бигбордах они вырастают до размеров человеческой головы, а на клоунском костюме уменьшаются до горошка. Поэтому добавьте реальности в свои представления о точках, пока вы не стали жертвой другой плохой привычки, мешающей креативному мышлению.
Речь идет об использовании узких определений, которые ограничивают процесс мышления наподобие воронки. Мы увязаем в старых парадигмах.
Благодаря отсутствующим границам, уточненным предположениям и расширенным определениям, мы нашли следующее решение проблемы 3 прямых:

Мысленно покиньте лист бумаги. Первая прямая проходит по касательной первую точку, пересекает вторую почти по центру и немного задевает третью точку. Продлите эту прямую дальше, за край бумаги, пока другая прямая не сможет проделать то же самое со средним столбцом точек. Аналогичным образом должна повести себя и третья прямая.
Вот решение, базирующееся на постулате неевклидовой геометрии о том, что параллельные прямые пересекаются в бесконечности. Ответ состоит из трех параллельных линий, каждая из которых затрагивает различные ряды точек, а затем все три линии соединяют в бесконечности. Аккуратный сдвиг парадигмы, не так ли? Вполне возможно, поиск решения потребует покинуть вашу зону комфорта.
Привычка, сводящая креативность к нулю: зачастую мы выделяем “справедливую” идею еще до того, как сделать выбор из нескольких решений. Не позволяйте “порядочности” мешать поискам.
Следующая проблема для 9 точек.

Задача: используйте 2 пересекающиеся прямые линии, которые коснутся всех 9 точек только 1 раз.
Невозможно, говорите вы? Вам не помешает еще одна ревизия своих необоснованных предположений, несуществующих границ, надуманных критериев, узких определений, мыслительных воронок и шаблонов.
Один блок таится в определении линии, которого вы придерживаетесь. Из школьной программы: линия - это бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца, т.е. обладают только одним свойством - длиной. В реальной жизни у линий есть ширина. Вспомните потоки транспорта на магистралях или цепочку из троллейбусов перед перекрестком. Таким образом, и на этот раз, склонность к готовым терминам привела вас к выводу, что можно использовать лишь тонкие линии.
Вот что получается, если определения расширить - решение, состоящее из одной широкой и одной узкой линий!

В поисках решения нашей последней проблемы попробуйте воспользоваться техникой “вынужденного ухода”.
Задача: одна прямая линия должна коснуться всех девяти точек.
Найдите, как минимум, 15 ответов, прежде, чем читать дальше.
Вообще, существует не меньше сотни приемлемых решений. Некоторые из них приведены здесь, чтобы вызвать новые парадигмы и мыслительные воронки и подогреть аппетит к большему.
По материалам книги "R&D CREATIVITY & INNOVATION HANDBOOK" A Practical Guide To Improve Creative Thinking & Innovation By Edward Glassman, PH.D.
Вот они – 9 магических точек:

Задача: не отрывая карандаша от бумаги, провести 4 пересекающиеся прямые линии, которые коснутся всех девяти точек только 1 раз.
Потратьте на поиск решения не менее 5 минут, прежде, чем читать дальше.
Если у вас ничего не вышло, подумайте о том, что вы видите, глядя на эти 9 точек? Если вы представляете себе квадрат, треугольники или другие геометрические фигуры, то вы блокируете свое мышление, рисуя границы, которых нет. Вы удерживаете себя внутри линий, которых не существует.
Привычка, сводящая креативность к нулю: мы слишком часто возводим границы, которых на самом деле нет. И мы остаемся в них. Мы играем по этим правилам. Мы пользуемся фантомными критериями. Мы прогнозируем развитие проекта, основываясь на тенденциях и возможностях, имевших место в прошлом, без поиска и сопоставления новых. Мы не отбрасываем сложившуюся парадигму без разрешения.
Вы могли бы соединить точки четырьмя линиями, выйдя за рамки квадрата. Вот так:
Как вам решение? Нравится? Не кажется ли оно вам элегантным и единственно возможным? На самом деле, самым серьезным ограничением в решении этой задачи является как раз вывод, что существует только ОДИН ответ. В действительности же вы можете отыскать несколько абсолютно разных решений этой проблемы.
Но как сломать парадигму и найти другие результаты?
Есть техника, которая называется «вынужденный уход». Нужно забыть о постановке проблемы и работать над решением ее дистанцированной версии. Это путь к новым парадигмам, перспективам и результатам.
И первой модифицированной задачей будет… те же 9 точек
Задача: на этот раз проведите 3 пересекающиеся прямые линии, которые должны коснуться каждой точки только 1 раз. Если не удается найти решение, постарайтесь определить, какие рамки, выводы и критерии вам мешают и останавливают поиск.
Давайте посмотрим вместе.
Во-первых, скажите, что вы видите, глядя на область точек? Надеюсь, вы уже отказались от привычки рисовать квадрат и другие фигуры. Теперь вас, возможно, блокирует то, что вы видите эти точки на листе бумаги. Для того, чтобы найти несколько способов решения проблемы «3 линий», вам нужно представить эти точек в пространстве. Только так 3 прямые смогут покинуть кусок бумаги.
Во, вторых, не кажется ли вам, что эти линии должны проходить через центр каждой из 9 точек? Это несуществующее условие мешает вам думать.
В-третьих, как вы определяете саму точку? В школе нас учили, что точка – это элемент геометрического пространства, характеризуется только положением, принадлежностью, а не размером или формой. А вот эти кружочки, которые в нашей задаче называются точками, как раз имеют и форму, и размер. Не совсем честно с нашей стороны, да? Ну что ж, такова жизнь. А в реальной жизни точки очень разнятся по величине и форме. На бигбордах они вырастают до размеров человеческой головы, а на клоунском костюме уменьшаются до горошка. Поэтому добавьте реальности в свои представления о точках, пока вы не стали жертвой другой плохой привычки, мешающей креативному мышлению.
Речь идет об использовании узких определений, которые ограничивают процесс мышления наподобие воронки. Мы увязаем в старых парадигмах.
Благодаря отсутствующим границам, уточненным предположениям и расширенным определениям, мы нашли следующее решение проблемы 3 прямых:
Мысленно покиньте лист бумаги. Первая прямая проходит по касательной первую точку, пересекает вторую почти по центру и немного задевает третью точку. Продлите эту прямую дальше, за край бумаги, пока другая прямая не сможет проделать то же самое со средним столбцом точек. Аналогичным образом должна повести себя и третья прямая.
Вот решение, базирующееся на постулате неевклидовой геометрии о том, что параллельные прямые пересекаются в бесконечности. Ответ состоит из трех параллельных линий, каждая из которых затрагивает различные ряды точек, а затем все три линии соединяют в бесконечности. Аккуратный сдвиг парадигмы, не так ли? Вполне возможно, поиск решения потребует покинуть вашу зону комфорта.
Привычка, сводящая креативность к нулю: зачастую мы выделяем “справедливую” идею еще до того, как сделать выбор из нескольких решений. Не позволяйте “порядочности” мешать поискам.
Следующая проблема для 9 точек.
Задача: используйте 2 пересекающиеся прямые линии, которые коснутся всех 9 точек только 1 раз.
Невозможно, говорите вы? Вам не помешает еще одна ревизия своих необоснованных предположений, несуществующих границ, надуманных критериев, узких определений, мыслительных воронок и шаблонов.
Один блок таится в определении линии, которого вы придерживаетесь. Из школьной программы: линия - это бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца, т.е. обладают только одним свойством - длиной. В реальной жизни у линий есть ширина. Вспомните потоки транспорта на магистралях или цепочку из троллейбусов перед перекрестком. Таким образом, и на этот раз, склонность к готовым терминам привела вас к выводу, что можно использовать лишь тонкие линии.
Вот что получается, если определения расширить - решение, состоящее из одной широкой и одной узкой линий!
В поисках решения нашей последней проблемы попробуйте воспользоваться техникой “вынужденного ухода”.
Задача: одна прямая линия должна коснуться всех девяти точек.
Найдите, как минимум, 15 ответов, прежде, чем читать дальше.
Вообще, существует не меньше сотни приемлемых решений. Некоторые из них приведены здесь, чтобы вызвать новые парадигмы и мыслительные воронки и подогреть аппетит к большему.
- Используйте одну широкую линию, которая касается каждой точки.
- Пропустите большую 3-мерную линию через девять точек сверху вниз так, что она пройдет через бумагу и коснется каждой точки.
- Сложите бумагу так что вы можете сделать одну линию, которая касается каждой точки. (Вы предполагали, что вам запрещалось сложить бумагу?)
- Разрежьте бумагу так, чтобы каждая точка оказалась на отдельном клочке. Уложите частички в одну линию, которая затронет каждую точку. (Вы думали, что вы не можете резать бумагу?)
- Сверните лист бумаги в конус и нарисуйте прямую линию, что спирали вокруг поверхности конуса и затрагивает все девять точек. (Вам не приходило в голову, что с бумагой можно делать все, что угодно?)
- Положите лист бумаги с девятью точками на экватор Земли и тщательно рисуйте прямую линию вокруг Земли достаточное количество раз, так что в итоге она коснется каждой точки. Или положите бумагу на край Вселенной и проводите вашу прямую кольцевую линию вокруг Вселенной, пока она не коснется каждой точки. (Вы не предполагали, что вы можете использовать фантазию? Обратите внимание, мы расширили нашу мыслительную воронку из девяти точек до окна, выходящего на край Вселенной).
- Напишите "ОДНА" поверх первого ряда точек, "ПРЯМАЯ” над средним рядом точек и "ЛИНИЯ" над нижней строкой точек. Вы коснулись точек словами "одна прямая линия" (Вы думали, что вы не можете использовать слова?)
- Нарисуйте линию на тонком краю бумаги. Посмотреть на девять точек через эту боковую линию.
- Перемещайте прямую, как стеклоочистители в автомобиле, - и вы коснетесь всех точек. (Вам казалось, что вы не могли двигать линию, или что линия должна была коснуться всех точек в одно и то же время?)
- Разрежьте прямую линию на 1000 кусочков и рассыпьте их над девятью точками (А что, было запрещено разрезать линии?)
- Разрежьте так, чтобы одна точка оказалась на отдельном кусочке бумаги. Выстройте точки в башенку, одну над другой. Нажмите карандашом на все точки. Вы не только коснулись всех точек одной прямой, но вы уничтожили и точки, и проблемы. Одним махом.
- Подождите. Вот еще одна затравка для размышлений. Представьте, вы сидите со своими точками за столом, и тут входит царь зверей и проглатывает их все разом. Или как насчет девяти человек, каждого из которых зовут Точка, съеденных одним львом?
- Не могу удержаться от еще более странного решения. Измененить точки в прищепки и повесить их на одной прямой бельевой веревке. (Вы предположили, что не можете конвертировать точки или линии во что-то еще?)
- Или можно превратить точки в теннисные мячи и играть в теннис с ними, пока каждый из них не коснется теннисной сетки, которая является одной прямой линией.
- Или изменить линию в тень солнечных часов, чтобы он в конечном итоге коснется всех точек, как Солнце движется по небу.
- Или преобразовать прямую в солнечный луч и использовать стеклянную призму, чтобы разбить ее на множество цветных линий, которые касаются всех девяти точек. Пока хватит?
По материалам книги "R&D CREATIVITY & INNOVATION HANDBOOK" A Practical Guide To Improve Creative Thinking & Innovation By Edward Glassman, PH.D.
No comments:
Post a Comment